Applied ANOVA in R
Navigating the R linear model wilderness

Introduction
ANOVA in R is a unfortunately a bit complicated. Unlike SAS, ANOVA functions in R lack a consistent structure, consistent output and the accessory packages for ANOVA display a patchwork of compatibility. The result is that it is easy to misspecify a model or make other mistakes. The information below is intended to serve as a guide through the R ANOVA wilderness.
Packages Needed
There are many packages to load. Here is a (very) brief summary of what each package does.
| Package | Purpose |
|---|---|
| car | Anova() function to extract type III & II sums of squares |
| lme4 | mixed models |
| nlme | mixed models, non-linear models, alternative covariance structures |
| emmeans | for extracting least squares means and contrasts |
| lmer test | improved summary functions of lmer objects |
| dplyr | data organization |
| forcats | for managing categorical data |
| agridat | has many agricultural data sets |
| agricolae | has options for many common agricultural experimental designs |
library(car)
library(lme4)
library(nlme)
library(emmeans) #in older version of R, you may need to install "multcompView" separately to access full functionality of the emmeans package
library(lmerTest)
library(dplyr)
library(forcats)
library(agridat)
Formula Notation
There are some consistent features across ANOVA methods in R. Formula notation is often used in the R syntax for ANOVA functions. It looks like this: $Y ~ X, where Y is the dependent variable (the response) and X is/are the independent variable(s) (e.g. the experimental treatments).
my_formula <- formula(Y ~ treatment1 + treatment2)
class(my_formula)
## [1] "formula"
my_formula
## Y ~ treatment1 + treatment2
Often the independent variables (i,e, the treatments or the x variables) are expected to be factors, another type of R object:
my_var <- c(rep("low",5), rep("high", 5))
class(my_var) #check what variable type it is
## [1] "character"
Although “my_var” is not type factor, it is type “character” which is automatically converted to a factor in lm(), lmer(), lme() and many other linear modeling functions. There are some packages that do not follow this convention, so it’s helpful to read function documentation, especially if you get unexpected results.
Variables like year, which are often imported as a number or integer, do need to be converted to a factor or a character variable prior to analysis. Otherwise, they will be interpreted as a number in linear modelling and treated as a covariate, e.g, 2020 would be 2,020. Here is one way to do this conversion:
my_factor <- as.character(my_var) # convert to a character
class(my_factor) # check variable type to confirm
## [1] "character"
my_factor <- as.factor(my_var) # convert to a factor
class(my_factor) # check variable type again to confirm
## [1] "factor"
The choice of whether to convert a categorical variable to a character or factor depends on the comfort of the user with these structures and package requirements.
Sometimes, there is a need to alter the order of treatment levels (that is, how R sees those levels). The default behavior of R is to order categorical levels alphanumerically. However, sometimes there are reasons you may not want this (for example, you want to set a particular reference level as the first factor level).
Below is one example of how to reorder factor levels in a variable. The first step is to see which levels are present in the variable and how they are ordered:
levels(my_factor)
## [1] "high" "low"
Once that is known, you can use that information to manually set the levels and their order. Note that spelling of each level much match what is actually present in the variable. Unmatched levels in the variable will be set to NA automatically by R in the following step.
my_factor <- factor(my_factor, levels = c("low", "high"))
levels(my_factor) # check the new ordering
## [1] "low" "high"
Knowing the level order is important because in the implementation of ANOVA in R, the first level is treated as the reference level. Manipulating factors is a challenging task in R. The package forcats contains a collection of accessory functions for managing factors (“forcats” = for categories). The tutorial uses the forcats function fct_drop().
More on formulas:
The formula first shown, Y ~ treatment1 + treatment2, includes main effects only. Other formula notation includes the symbols : and *, indicating notation for interaction only and main effects plus the interaction term, respectively.
formula(Y ~ treatment1:treatment2) # interaction only
## Y ~ treatment1:treatment2
formula(Y ~ treatment1*treatment2) # interaction plus main effects
## Y ~ treatment1 * treatment2
These two formulas are equivalent:
formula(Y ~ treatment1 + treatment2 + treatment1:treatment2)
formula(Y ~ treatment1*treatment2)
Perhaps you can see from these examples that formulas are a really just a collections of characters (that is, a string) and exist independent of any data set. Later, we will need to link these formulas to a data set to actually construct a linear model and conduct statistical analysis.
ANOVA for fixed effects models
Here is a function for reporting the number of missing data in each column. There are other ways to do this, but I find this function easy enough to write and use.
count_na <- function(df) {
apply(df, 2, function(x) sum(is.na(x)))
}
Completely Randomised design
First, load the data set “warpbreaks” (a data set from base R). This is an old data set with variables for wool type (A and B) and tension on the loom (L, M or H). The response variable is “breaks”, the number of times the wool thread breaks on industrial looms.
I always like to have a quick look at the data before running any statistical tests. So, here we go:
data(warpbreaks)
count_na(warpbreaks)
## breaks wool tension
## 0 0 0
str(warpbreaks)
## 'data.frame': 54 obs. of 3 variables:
## $ breaks : num 26 30 54 25 70 52 51 26 67 18 ...
## $ wool : Factor w/ 2 levels "A","B": 1 1 1 1 1 1 1 1 1 1 ...
## $ tension: Factor w/ 3 levels "L","M","H": 1 1 1 1 1 1 1 1 1 2 ...
warpbreaks$wool <- factor(warpbreaks$wool, levels = c("A", "B", "C"))
table(warpbreaks$wool, warpbreaks$tension)
##
## L M H
## A 9 9 9
## B 9 9 9
## C 0 0 0
hist(warpbreaks$breaks, col = "gold")

boxplot(breaks ~ wool, data = warpbreaks, col = "orangered")

boxplot(breaks ~ tension, data = warpbreaks, col = "chartreuse") #why not have colorful plots?

This data set has 2 treatments. We don’t know if there is an interaction between the variables, yet. A good start is to run a linear model using lm() function, the linear regression function. As a reminder, ANOVA is a special case of the linear regression model where the predictors (the experimental treatments) are categories rather than a continuous variable.
# run standard linear model for main effects only
lm.mod1 <- lm(breaks ~ wool + tension, data = warpbreaks)
# extract type III sums of squares from that model
Anova(lm.mod1, type = "3")
## Anova Table (Type III tests)
##
## Response: breaks
## Sum Sq Df F value Pr(>F)
## (Intercept) 20827.0 1 154.3226 < 2.2e-16 ***
## wool 450.7 1 3.3393 0.073614 .
## tension 2034.3 2 7.5367 0.001378 **
## Residuals 6747.9 50
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# run a linear model with main effects and interactions
lm.mod2 <- lm(breaks ~ wool*tension, data = warpbreaks)
# ...and type III sums of squares
Anova(lm.mod2, type = "III")
## Anova Table (Type III tests)
##
## Response: breaks
## Sum Sq Df F value Pr(>F)
## (Intercept) 17866.8 1 149.2757 2.426e-16 ***
## wool 1200.5 1 10.0301 0.0026768 **
## tension 2468.5 2 10.3121 0.0001881 ***
## wool:tension 1002.8 2 4.1891 0.0210442 *
## Residuals 5745.1 48
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
FYI
functions only shown as an example and not actually run.
# this function runs type II sums of squares:
Anova(lm.mod2, type = "II")
# this function runs type I sums of squares:
anova(lm.mod2)
A few comments on types of sums of squares:
As a reminder, the type of sums of squares used in statistical tests can impact the results and subsequent interpretation. Type I, sums of squares tests for statistical significance by adding one variable to the model at time (and hence is also called “sequential”). If there is any unbalance in the treatments, the type I sums of squares are dependent on the order variables are added to the model and hence is often not the best choice for many agricultural experiment. Type III sums of squares (also called “partial” or “marginal”) evaluates the statistical significance of variable or interaction, assuming that the other variables are in the model. This is a decent default option. The last option is Type II sums of squares, which is the best option when you are sure there are no interactions between variables. If there is complete balance among treatments (each treatment is observed the same number of times with no missing data), then there is no need to concern yourself with these different types of sums of squares.
Compare Models
# conduct an F test comparing the models
anova(lm.mod1, lm.mod2)
## Analysis of Variance Table
##
## Model 1: breaks ~ wool + tension
## Model 2: breaks ~ wool * tension
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 50 6747.9
## 2 48 5745.1 2 1002.8 4.1891 0.02104 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# also, consider doing a stepwise approach for finding the best model:
step(lm.mod2)
## Start: AIC=264.02
## breaks ~ wool * tension
##
## Df Sum of Sq RSS AIC
## <none> 5745.1 264.02
## - wool:tension 2 1002.8 6747.9 268.71
##
## Call:
## lm(formula = breaks ~ wool * tension, data = warpbreaks)
##
## Coefficients:
## (Intercept) woolB tensionM tensionH woolB:tensionM
## 44.56 -16.33 -20.56 -20.00 21.11
## woolB:tensionH
## 10.56
Model diagnostics
plot(lm.mod2) #this will produce 4 plots of residuals



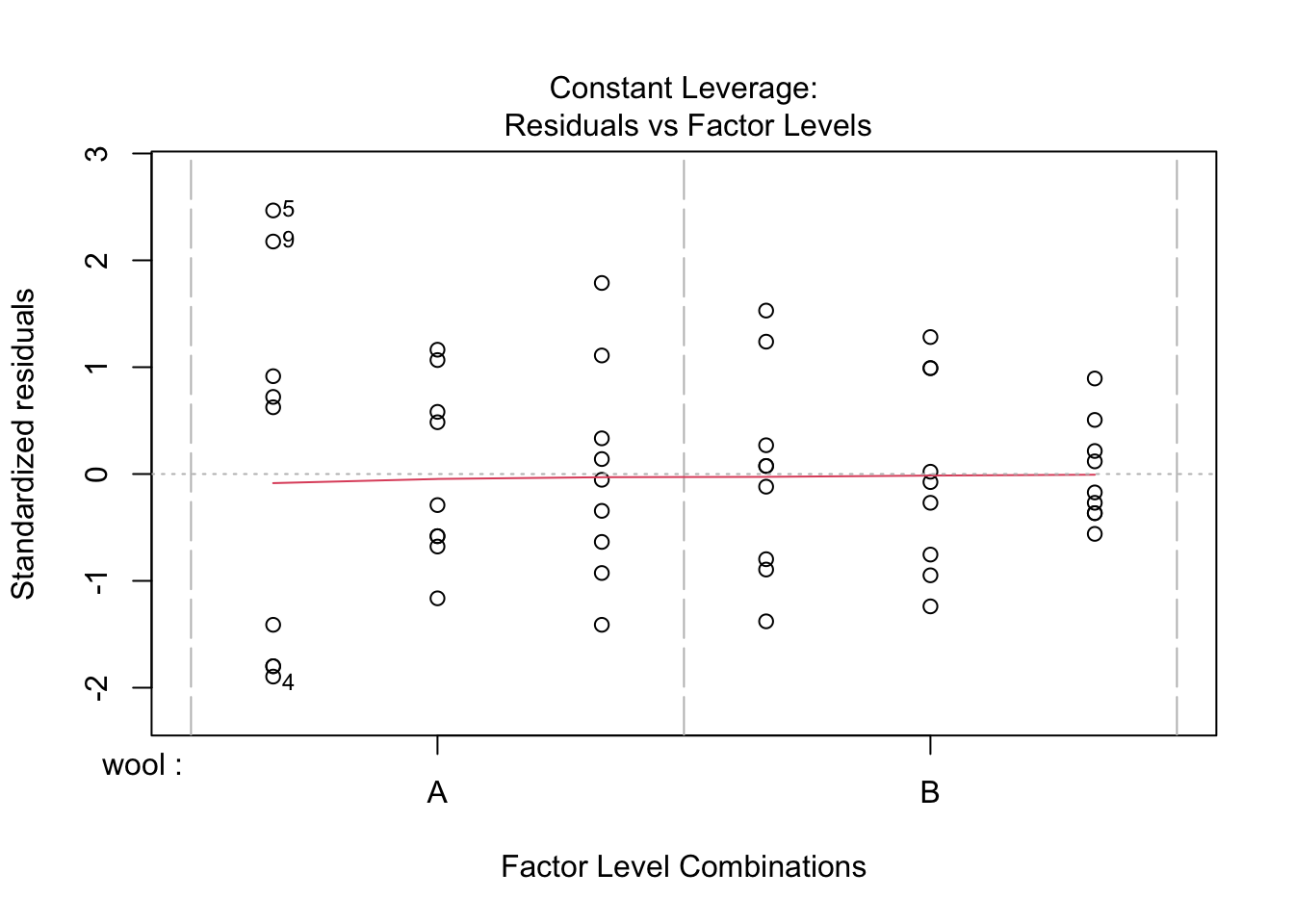
shapiro.test(resid(lm.mod2)) #standard shapiro-wilk test.
##
## Shapiro-Wilk normality test
##
## data: resid(lm.mod2)
## W = 0.98686, p-value = 0.8162
# this variable could be analyzed with a log-normal model instead
Least squares means & contrasts
The emmeans package is a flexible package for extracting the estimated marginal means (in SAS, the “least squares means”) from different linear models. It is compatible with a large number of R linear modelling packages.
Here is some code for extracting the marginal means and conducting contrasts.
# extract least squares means for 'tension'
(lsm <- emmeans(lm.mod2, ~ tension))
## NOTE: Results may be misleading due to involvement in interactions
## tension emmean SE df lower.CL upper.CL
## L 36.4 2.58 48 31.2 41.6
## M 26.4 2.58 48 21.2 31.6
## H 21.7 2.58 48 16.5 26.9
##
## Results are averaged over the levels of: wool
## Confidence level used: 0.95
emmeans(lm.mod2, "wool")
## NOTE: Results may be misleading due to involvement in interactions
## wool emmean SE df lower.CL upper.CL
## A 31.0 2.11 48 26.8 35.3
## B 25.3 2.11 48 21.0 29.5
##
## Results are averaged over the levels of: tension
## Confidence level used: 0.95
All pairwise comparisons within each level of tension:
contrast(lsm, "pairwise")
## contrast estimate SE df t.ratio p.value
## L - M 10.00 3.65 48 2.742 0.0229
## L - H 14.72 3.65 48 4.037 0.0006
## M - H 4.72 3.65 48 1.295 0.4049
##
## Results are averaged over the levels of: wool
## P value adjustment: tukey method for comparing a family of 3 estimates
Conduct custom contrasts comparing ‘Low’ tension versus ‘Medium’ and ‘High’ and ‘High’ versus ‘Medium’ and ‘Low’.
# see the order of each level in a factor
levels(warpbreaks$tension)
## [1] "L" "M" "H"
# construct a list of constructs
# each item must be same length as the the number of levels present in the variable tension
# use numbers and fracions to indicate the contrasting levels
# the numbers must sum to zero
cList <- list(LvMH = c(1, -0.5, -0.5), # low vs high + medium
HvLM = c(0.5, 0.5, -1)) # high vs low + medium
# check that each contrast sums to zero
lapply(cList, sum)
## $LvMH
## [1] 0
##
## $HvLM
## [1] 0
# perform custom contrast and include a Bonferroni adjustment
summary(contrast(lsm, cList, adjust = "bonferroni"))
## contrast estimate SE df t.ratio p.value
## LvMH 12.36 3.16 48 3.914 0.0006
## HvLM 9.72 3.16 48 3.078 0.0069
##
## Results are averaged over the levels of: wool
## P value adjustment: bonferroni method for 2 tests
Randomised Complete Block Design (RCBD) - fixed effects model
This example uses rapeseed yield data from multiple locations, years and cultivars. Within a single location or year, the replication is often balanced.
Load Data and examine:
data(shafii.rapeseed) # from the 'agridat' package
rapeseed1987 <- shafii.rapeseed %>% filter(year == 87) %>%
mutate(block = fct_drop(rep), Cv = fct_drop(gen), loc = fct_drop(loc))
str(rapeseed1987)
## 'data.frame': 216 obs. of 7 variables:
## $ year : int 87 87 87 87 87 87 87 87 87 87 ...
## $ loc : Factor w/ 9 levels "GGA","ID","MT",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ rep : Factor w/ 4 levels "R1","R2","R3",..: 1 2 3 4 1 2 3 4 1 2 ...
## $ gen : Factor w/ 6 levels "Bienvenu","Bridger",..: 1 1 1 1 2 2 2 2 3 3 ...
## $ yield: num 961 1329 1781 1698 1605 ...
## $ block: Factor w/ 4 levels "R1","R2","R3",..: 1 2 3 4 1 2 3 4 1 2 ...
## $ Cv : Factor w/ 6 levels "Bienvenu","Bridger",..: 1 1 1 1 2 2 2 2 3 3 ...
count_na(rapeseed1987)
## year loc rep gen yield block Cv
## 0 0 0 0 0 0 0
table(rapeseed1987$Cv, rapeseed1987$loc) #experiment has 1 rep per block
##
## GGA ID MT NC OR SC TGA TX WA
## Bienvenu 4 4 4 4 4 4 4 4 4
## Bridger 4 4 4 4 4 4 4 4 4
## Cascade 4 4 4 4 4 4 4 4 4
## Dwarf 4 4 4 4 4 4 4 4 4
## Glacier 4 4 4 4 4 4 4 4 4
## Jet 4 4 4 4 4 4 4 4 4
hist(rapeseed1987$yield, col = "gold")

boxplot(yield ~ Cv, data = rapeseed1987, col = "orangered")

boxplot(yield ~ loc, data = rapeseed1987, col = "chartreuse")

Analyse experiment:
# for this example, the analysis will only be done for a single year
# block is nested within location
# if each block had a unique name, 'Error(block)' would suffce
shaf.aov <- aov(yield ~ Cv*loc + Error(block), data = rapeseed1987)
summary(shaf.aov)
##
## Error: block
## Df Sum Sq Mean Sq F value Pr(>F)
## Residuals 3 336565 112188
##
## Error: Within
## Df Sum Sq Mean Sq F value Pr(>F)
## Cv 5 3203992 640798 2.645 0.025111 *
## loc 8 318197192 39774649 164.165 < 2e-16 ***
## Cv:loc 40 22707425 567686 2.343 0.000103 ***
## Residuals 159 38523267 242285
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
emmeans(shaf.aov, ~ Cv | loc)
## Note: re-fitting model with sum-to-zero contrasts
## loc = GGA:
## Cv emmean SE df lower.CL upper.CL
## Bienvenu 1442 245 161 959 1926
## Bridger 1363 245 161 880 1847
## Cascade 1505 245 161 1021 1988
## Dwarf 1295 245 161 811 1779
## Glacier 1681 245 161 1197 2164
## Jet 1091 245 161 607 1575
##
## loc = ID:
## Cv emmean SE df lower.CL upper.CL
## Bienvenu 1242 245 161 759 1726
## Bridger 947 245 161 463 1430
## Cascade 773 245 161 290 1257
## Dwarf 932 245 161 448 1415
## Glacier 1111 245 161 627 1595
## Jet 1064 245 161 580 1548
##
## loc = MT:
## Cv emmean SE df lower.CL upper.CL
## Bienvenu 2616 245 161 2132 3100
## Bridger 2828 245 161 2345 3312
## Cascade 2916 245 161 2433 3400
## Dwarf 3452 245 161 2968 3935
## Glacier 3307 245 161 2823 3790
## Jet 3660 245 161 3177 4144
##
## loc = NC:
## Cv emmean SE df lower.CL upper.CL
## Bienvenu 1001 245 161 517 1485
## Bridger 1064 245 161 581 1548
## Cascade 745 245 161 262 1229
## Dwarf 1014 245 161 530 1497
## Glacier 1229 245 161 746 1713
## Jet 1674 245 161 1190 2157
##
## loc = OR:
## Cv emmean SE df lower.CL upper.CL
## Bienvenu 4556 245 161 4072 5039
## Bridger 2530 245 161 2046 3013
## Cascade 3336 245 161 2852 3819
## Dwarf 3932 245 161 3448 4415
## Glacier 4185 245 161 3702 4669
## Jet 3220 245 161 2736 3703
##
## loc = SC:
## Cv emmean SE df lower.CL upper.CL
## Bienvenu 2500 245 161 2016 2983
## Bridger 2705 245 161 2221 3189
## Cascade 2119 245 161 1635 2602
## Dwarf 1894 245 161 1410 2377
## Glacier 2717 245 161 2234 3201
## Jet 2833 245 161 2349 3316
##
## loc = TGA:
## Cv emmean SE df lower.CL upper.CL
## Bienvenu 1258 245 161 774 1741
## Bridger 1868 245 161 1384 2351
## Cascade 1708 245 161 1224 2191
## Dwarf 873 245 161 389 1356
## Glacier 1453 245 161 970 1937
## Jet 954 245 161 470 1438
##
## loc = TX:
## Cv emmean SE df lower.CL upper.CL
## Bienvenu 838 245 161 354 1322
## Bridger 1069 245 161 585 1553
## Cascade 735 245 161 251 1218
## Dwarf 988 245 161 505 1472
## Glacier 952 245 161 468 1435
## Jet 1408 245 161 925 1892
##
## loc = WA:
## Cv emmean SE df lower.CL upper.CL
## Bienvenu 4375 245 161 3891 4859
## Bridger 4604 245 161 4120 5087
## Cascade 4464 245 161 3981 4948
## Dwarf 3974 245 161 3490 4458
## Glacier 4740 245 161 4256 5224
## Jet 4344 245 161 3861 4828
##
## Warning: EMMs are biased unless design is perfectly balanced
## Confidence level used: 0.95
ANOVA for mixed models
(models with random and fixed effects)
Random effects are often those treatments levels drawn from a large population of possible treatment levels and there is interest in understanding the distribution and variance of that population. This in contrast to fixed effects, where the inferences are restricted to the treatment levels tested.
Blocking factors and Year are often considered random factors because a researcher is not interested in particular years or a blocking factor. When there is unbalanced replication, the variance components should be estimated with maximum likelihood or REML, which implies use of the packages “lmer” and/or “nlme”.
Randomised Complete Block Design (RCBD) - mixed effects
The “shafii.rapeseed” data set will be used for this section.
Analyse experiment using a mixed model:
This uses the function lme() from the package “nlme”. Functionally, it is very similar to calling lme4::lmer(). The degrees of freedom are different (lmer() is using Satterthwaite’s approximation), but the p-values are the same.
# turn year into the factor "Year"
shafii.rapeseed$Year <- as.factor(shafii.rapeseed$year)
# create a blocking variable that is unique for each location-by-year combination
# so R doesn't conflate "R1" from one location/year with another location/year
shafii.rapeseed$Rep <- as.factor(paste(shafii.rapeseed$loc, shafii.rapeseed$year, shafii.rapeseed$rep, sep = "_"))
shaf.lme <- lme(fixed = yield ~ gen*loc + Year,
random = ~ 1|Rep,
data = shafii.rapeseed, method = "REML")
# view sum of squares table
# when anova() is called for an lme object, the function called is actually anova.lme()
anova(shaf.lme, type = "marginal") # "marginal" is equivalent to type III sums of squares
## numDF denDF F-value p-value
## (Intercept) 1 470 16.204597 0.0001
## gen 5 470 1.092341 0.3637
## loc 13 92 13.074492 <.0001
## Year 2 92 2.035054 0.1365
## gen:loc 65 470 2.575753 <.0001
Anova(shaf.lme, type = "3")
## Analysis of Deviance Table (Type III tests)
##
## Response: yield
## Chisq Df Pr(>Chisq)
## (Intercept) 16.2046 1 5.686e-05 ***
## gen 5.4617 5 0.3622
## loc 169.9684 13 < 2.2e-16 ***
## Year 4.0701 2 0.1307
## gen:loc 167.4239 65 5.579e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# FYI: use "anova(model.lme)" for type I sums of squares
# lmer notation
shaf.lmer <- lmer(yield ~ gen*loc + Year + (1|Rep),
data = shafii.rapeseed, REML = T)
anova(shaf.lmer, type = "marginal")
## Marginal Analysis of Variance Table with Satterthwaite's method
## Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
## gen 1860586 372117 5 470.00 1.0923 0.3637
## loc 57901484 4453960 13 159.37 13.0745 < 2.2e-16 ***
## Year 1386524 693262 2 92.00 2.0351 0.1365
## gen:loc 57034691 877457 65 470.00 2.5758 5.499e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Anova(shaf.lmer, type = "3")
## Analysis of Deviance Table (Type III Wald chisquare tests)
##
## Response: yield
## Chisq Df Pr(>Chisq)
## (Intercept) 16.2046 1 5.686e-05 ***
## gen 5.4617 5 0.3622
## loc 169.9684 13 < 2.2e-16 ***
## Year 4.0701 2 0.1307
## gen:loc 167.4239 65 5.579e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Diagnostics, model building
plot(shaf.lme)

qqnorm(shaf.lme, abline = c(0, 1))
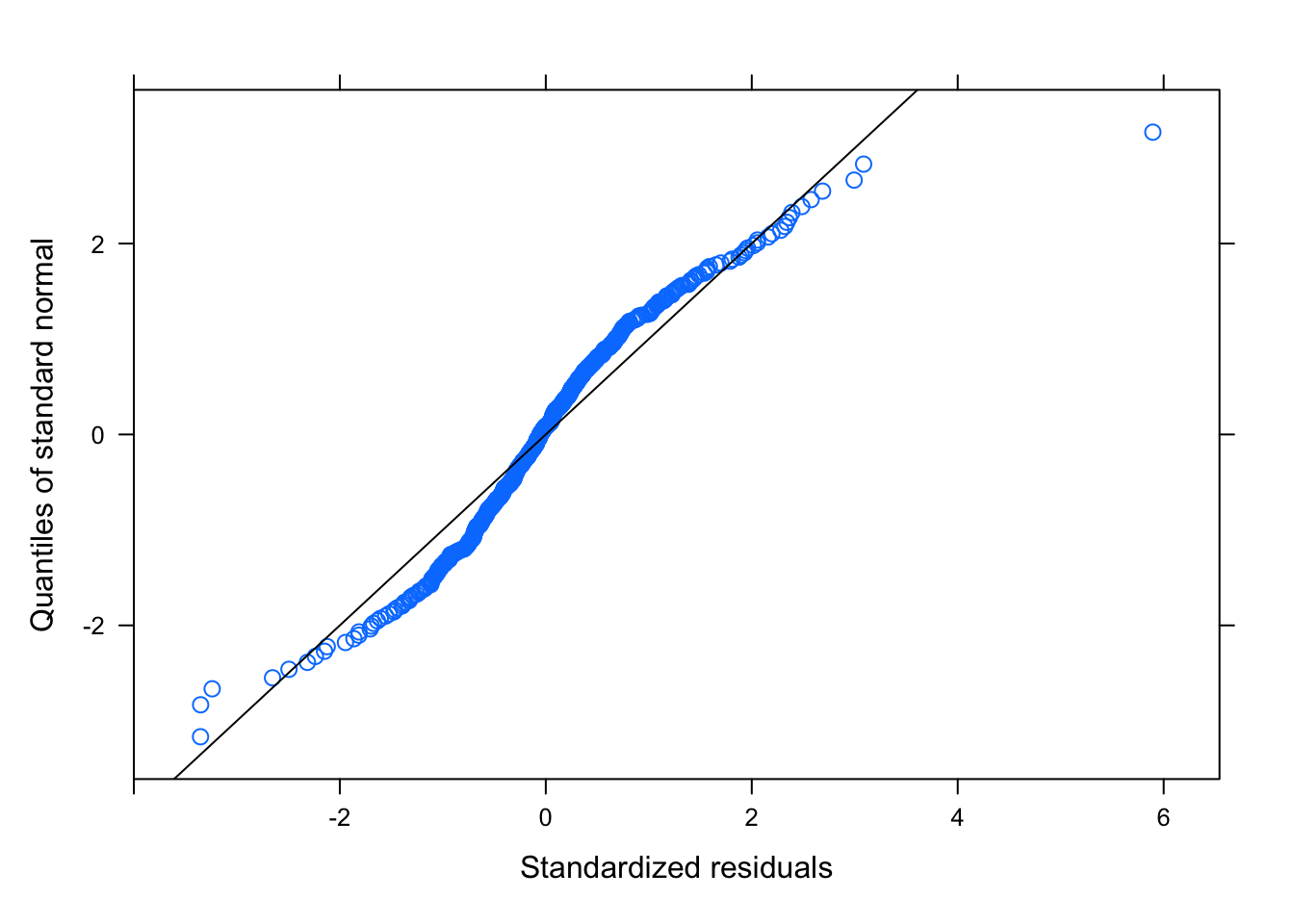
Least squares means
# for cultivar
(lme.means.cv <- emmeans(shaf.lme, "gen"))
## NOTE: Results may be misleading due to involvement in interactions
## gen emmean SE df lower.CL upper.CL
## Bienvenu 2432 112 92 2211 2654
## Bridger 2314 112 92 2092 2536
## Cascade 2184 112 92 1962 2406
## Dwarf 2308 112 92 2087 2530
## Glacier 2463 112 92 2242 2685
## Jet 2304 112 92 2082 2525
##
## Results are averaged over the levels of: loc, Year
## Degrees-of-freedom method: containment
## Confidence level used: 0.95
# for location
(lme.means.loc <- emmeans(shaf.lme, "loc"))
## NOTE: Results may be misleading due to involvement in interactions
## loc emmean SE df lower.CL upper.CL
## GGA 1682 329 92 1030 2335
## ID 4217 261 92 3698 4736
## KS 1120 476 92 174 2066
## MS 2204 476 92 1258 3150
## MT 3339 474 92 2398 4280
## NC 1328 329 92 676 1981
## NY 3139 476 92 2193 4085
## OR 3292 329 92 2640 3945
## SC 1819 261 92 1300 2338
## TGA 1028 261 92 509 1547
## TN 2543 476 92 1597 3490
## TX 827 329 92 174 1479
## VA 2282 328 92 1631 2932
## WA 3861 261 92 3342 4380
##
## Results are averaged over the levels of: gen, Year
## Degrees-of-freedom method: containment
## Confidence level used: 0.95
# for cultivar means within each location
lme.means.int <- emmeans(shaf.lme, ~ gen | loc + Year)
# this code would produce location means within each cultivar
# emmeans(model.lme, ~ loc | gen))
# also:
# emmeans(model.lme, ~ loc | gen)) provides the same estimates as 'emmeans(model.lme, ~ gen | loc))'
Pairwise Contrasts:
# all pairwise
pairs(lme.means.cv)
## contrast estimate SE df t.ratio p.value
## Bienvenu - Bridger 118.57 87.6 470 1.353 0.7548
## Bienvenu - Cascade 248.34 87.6 470 2.834 0.0539
## Bienvenu - Dwarf 124.11 87.6 470 1.417 0.7170
## Bienvenu - Glacier -31.00 87.6 470 -0.354 0.9993
## Bienvenu - Jet 128.70 87.6 470 1.469 0.6843
## Bridger - Cascade 129.77 87.6 470 1.481 0.6765
## Bridger - Dwarf 5.54 87.6 470 0.063 1.0000
## Bridger - Glacier -149.57 87.6 470 -1.707 0.5277
## Bridger - Jet 10.13 87.6 470 0.116 1.0000
## Cascade - Dwarf -124.23 87.6 470 -1.418 0.7161
## Cascade - Glacier -279.34 87.6 470 -3.188 0.0190
## Cascade - Jet -119.64 87.6 470 -1.366 0.7477
## Dwarf - Glacier -155.10 87.6 470 -1.770 0.4861
## Dwarf - Jet 4.59 87.6 470 0.052 1.0000
## Glacier - Jet 159.70 87.6 470 1.823 0.4521
##
## Results are averaged over the levels of: loc, Year
## Degrees-of-freedom method: containment
## P value adjustment: tukey method for comparing a family of 6 estimates
# plot results
plot(lme.means.cv, comparison = T)

plot(lme.means.loc, comparison = T, horizontal = F) # rotate plots to vertical position
## Warning: Comparison discrepancy in group "1", GGA - OR:
## Target overlap = 0.0083, overlap on graph = -0.0111

# blue bars = lsmeans confidence 95% confidence intervals
# red arrows. pairwise differences (overlapping arrows = not significantly different)
For those who want the letters assigned to treatments based on all pairwise comparisons, it’s an unwieldy road:
library(multcomp) # this will need to be installed if you do not already have it
tukey <- glht(shaf.lme, linfct = mcp(loc = "Tukey"))
### extract information
cld_tukey <- cld(tukey)
print(cld_tukey)
## GGA ID KS MS MT NC NY OR SC TGA TN TX VA WA
## "a" "b" "a" "ac" "ab" "a" "ab" "bc" "a" "a" "ab" "a" "a" "bc"
Interaction plots can also be done:
(but, it gets unwieldy)
plot(lme.means.int, comparison = T, adjust = "tukey")
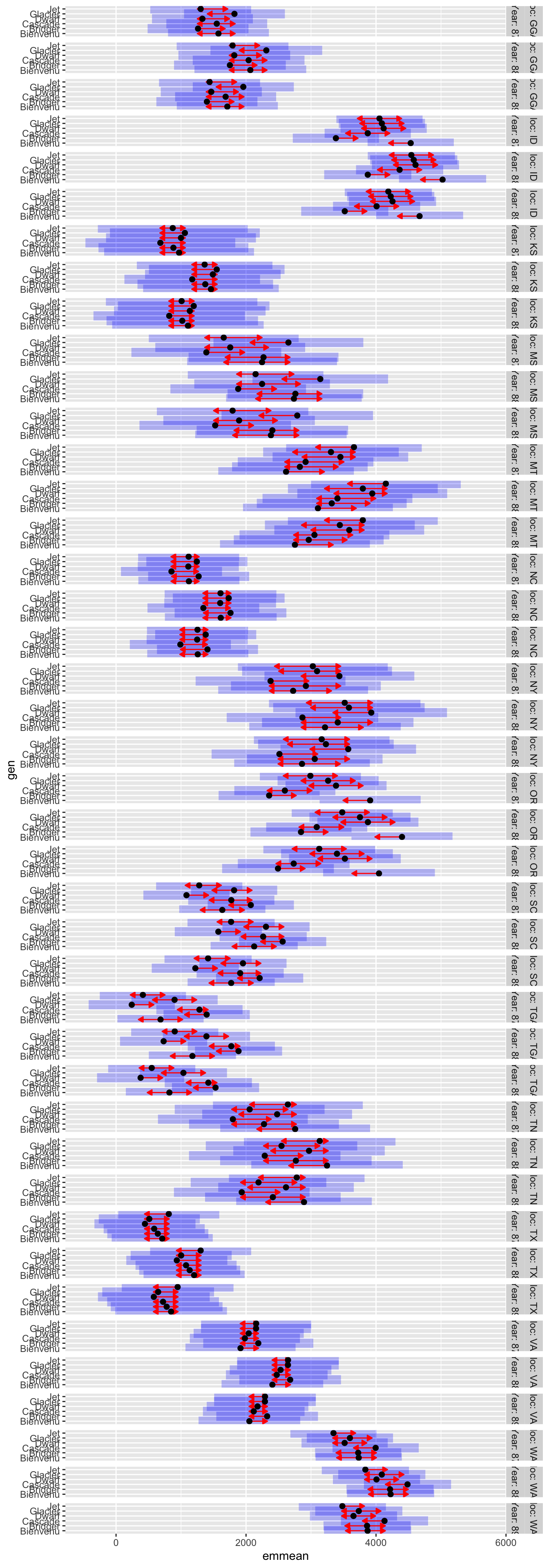
Other pre-set contrasts
# compare to a control, e.g. "Bridger"
levels(shafii.rapeseed$gen)
## [1] "Bienvenu" "Bridger" "Cascade" "Dwarf" "Glacier" "Jet"
# Bridger is listed in position 2 of the factor 'shafii.rapeseed$gen'
# so '2' is set as the reference level in the following contrast statement:
# "trt.vs.ctrlk" (treatment versus control treatment k) is a specific option to compare all treatment levels to a user-defined level
# by default, it will use the last level as the reference level
contrast(lme.means.cv, "trt.vs.ctrlk", ref = 2)
## contrast estimate SE df t.ratio p.value
## Bienvenu - Bridger 118.57 87.6 470 1.353 0.5118
## Cascade - Bridger -129.77 87.6 470 -1.481 0.4315
## Dwarf - Bridger -5.54 87.6 470 -0.063 0.9998
## Glacier - Bridger 149.57 87.6 470 1.707 0.3034
## Jet - Bridger -10.13 87.6 470 -0.116 0.9990
##
## Results are averaged over the levels of: loc, Year
## Degrees-of-freedom method: containment
## P value adjustment: dunnettx method for 5 tests
Search ?contrast.emmGrid to see full list of options for preset contrasts.
Custom contrasts
# example: contrast Western locations versus Southern locations
# first, find out what levels are present
unique(shafii.rapeseed$loc)
## [1] GGA ID KS MS MT NC NY OR SC TGA TN TX VA WA
## Levels: GGA ID KS MS MT NC NY OR SC TGA TN TX VA WA
# next create a contrast list
# this is a list of coefficients as long your list of treatment levels
# indicating what coefficients to give each treatment level
# in this example, levels "ID", "MT", "OR", and "WA" are contrasted versus
# "NC", "SC", "MS", "TN", "TX" and "VA"
cList <- list(West_V_South = c(0, 1/4, 0, -1/6, 1/4, -1/6, 0, 1/4, -1/6, 0, -1/6, -1/6, -1/6, 1/4))
# check that each contrast sums to zero:
lapply(cList, sum)
## $West_V_South
## [1] 5.551115e-17
lme.means.loc2 <- emmeans(shaf.lme, "loc", contr = cList)
## NOTE: Results may be misleading due to involvement in interactions
summary(lme.means.loc2)
## $emmeans
## loc emmean SE df lower.CL upper.CL
## GGA 1682 329 92 1030 2335
## ID 4217 261 92 3698 4736
## KS 1120 476 92 174 2066
## MS 2204 476 92 1258 3150
## MT 3339 474 92 2398 4280
## NC 1328 329 92 676 1981
## NY 3139 476 92 2193 4085
## OR 3292 329 92 2640 3945
## SC 1819 261 92 1300 2338
## TGA 1028 261 92 509 1547
## TN 2543 476 92 1597 3490
## TX 827 329 92 174 1479
## VA 2282 328 92 1631 2932
## WA 3861 261 92 3342 4380
##
## Results are averaged over the levels of: gen, Year
## Degrees-of-freedom method: containment
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## West_V_South 1843 233 92 7.910 <.0001
##
## Results are averaged over the levels of: gen, Year
## Degrees-of-freedom method: containment
# same contrast can also be done within each level of 'gen':
emmeans(shaf.lme, ~ loc | gen, contr = cList)
## $emmeans
## gen = Bienvenu:
## loc emmean SE df lower.CL upper.CL
## GGA 1785 379 92 1032.31 2537
## ID 4742 303 92 4140.13 5345
## KS 1179 546 92 94.60 2263
## MS 2455 546 92 1371.47 3539
## MT 2825 544 92 1745.38 3904
## NC 1330 379 92 577.36 2082
## NY 2934 546 92 1849.69 4018
## OR 4118 379 92 3365.98 4870
## SC 1844 303 92 1241.42 2446
## TGA 893 303 92 290.99 1496
## TN 2965 546 92 1880.59 4049
## TX 919 379 92 167.04 1671
## VA 2124 378 92 1373.34 2875
## WA 3943 303 92 3340.44 4545
##
## gen = Bridger:
## loc emmean SE df lower.CL upper.CL
## GGA 1470 379 92 718.17 2223
## ID 3591 303 92 2989.15 4194
## KS 1091 546 92 7.35 2175
## MS 2478 546 92 1393.89 3562
## MT 3037 544 92 1957.63 4117
## NC 1479 379 92 727.28 2232
## NY 3130 546 92 2045.60 4214
## OR 2564 379 92 1811.99 3316
## SC 2282 303 92 1679.58 2884
## TGA 1603 303 92 1000.66 2205
## TN 2485 546 92 1401.33 3569
## TX 851 379 92 99.08 1604
## VA 2397 378 92 1646.76 3148
## WA 3935 303 92 3332.27 4537
##
## gen = Cascade:
## loc emmean SE df lower.CL upper.CL
## GGA 1758 379 92 1006.25 2511
## ID 4081 303 92 3479.04 4684
## KS 891 546 92 -193.40 1975
## MS 1598 546 92 514.04 2682
## MT 3125 544 92 2045.63 4205
## NC 1062 379 92 309.61 1814
## NY 2586 546 92 1502.21 3670
## OR 2806 379 92 2053.82 3558
## SC 1982 303 92 1379.70 2584
## TGA 1492 303 92 889.83 2094
## TN 2006 546 92 922.37 3090
## TX 796 379 92 43.59 1548
## VA 2191 378 92 1440.56 2942
## WA 4203 303 92 3600.69 4805
##
## gen = Dwarf:
## loc emmean SE df lower.CL upper.CL
## GGA 1538 379 92 785.71 2290
## ID 4326 303 92 3723.81 4928
## KS 1208 546 92 123.85 2292
## MS 1966 546 92 881.69 3050
## MT 3661 544 92 2581.14 4740
## NC 1321 379 92 568.53 2073
## NY 3645 546 92 2561.26 4729
## OR 3594 379 92 2841.40 4346
## SC 1292 303 92 690.10 1895
## TGA 451 303 92 -151.81 1053
## TN 2688 546 92 1603.57 3771
## TX 654 379 92 -98.64 1406
## VA 2250 378 92 1499.12 3000
## WA 3726 303 92 3123.52 4328
##
## gen = Glacier:
## loc emmean SE df lower.CL upper.CL
## GGA 2031 379 92 1278.35 2783
## ID 4299 303 92 3696.61 4901
## KS 1268 546 92 183.85 2352
## MS 2861 546 92 1776.82 3945
## MT 3516 544 92 2436.14 4595
## NC 1452 379 92 699.82 2204
## NY 3301 546 92 2217.49 4385
## OR 3472 379 92 2719.36 4224
## SC 2025 303 92 1422.97 2628
## TGA 1109 303 92 506.90 1712
## TN 2265 546 92 1180.58 3348
## TX 720 379 92 -31.85 1473
## VA 2363 378 92 1612.64 3114
## WA 3807 303 92 3205.02 4410
##
## gen = Jet:
## loc emmean SE df lower.CL upper.CL
## GGA 1511 379 92 758.95 2263
## ID 4262 303 92 3659.68 4864
## KS 1082 546 92 -2.40 2166
## MS 1866 546 92 781.68 2950
## MT 3869 544 92 2789.89 4949
## NC 1326 379 92 573.58 2078
## NY 3237 546 92 2152.80 4321
## OR 3199 379 92 2446.70 3951
## SC 1488 303 92 886.13 2091
## TGA 622 303 92 19.27 1224
## TN 2853 546 92 1768.63 3937
## TX 1020 379 92 267.99 1772
## VA 2364 378 92 1613.85 3115
## WA 3554 303 92 2952.19 4157
##
## Results are averaged over the levels of: Year
## Degrees-of-freedom method: containment
## Confidence level used: 0.95
##
## $contrasts
## gen = Bienvenu:
## contrast estimate SE df t.ratio p.value
## West_V_South 1968 267 92 7.359 <.0001
##
## gen = Bridger:
## contrast estimate SE df t.ratio p.value
## West_V_South 1286 267 92 4.811 <.0001
##
## gen = Cascade:
## contrast estimate SE df t.ratio p.value
## West_V_South 1948 267 92 7.286 <.0001
##
## gen = Dwarf:
## contrast estimate SE df t.ratio p.value
## West_V_South 2132 267 92 7.972 <.0001
##
## gen = Glacier:
## contrast estimate SE df t.ratio p.value
## West_V_South 1826 267 92 6.828 <.0001
##
## gen = Jet:
## contrast estimate SE df t.ratio p.value
## West_V_South 1902 267 92 7.112 <.0001
##
## Results are averaged over the levels of: Year
## Degrees-of-freedom method: containment
To perform custom contrasts on a another variable, a cList and emmeans call for that variable is required.
ANCOVA
(analysis of covariance) From a R programming perspective, this is no different than running a standard linear model. A data set from agridat, “theobald.covariate” comparing corn silage yields across multiple years, locations and cultivars. The data set includes a covariate, “chu” (corn heat units, a bit like growing degree days).
Load data and examine:
data(theobald.covariate)
str(theobald.covariate)
## 'data.frame': 256 obs. of 5 variables:
## $ year : int 1990 1990 1990 1990 1990 1991 1991 1991 1991 1991 ...
## $ env : Factor w/ 7 levels "E1","E2","E3",..: 1 2 3 4 7 1 2 3 4 5 ...
## $ gen : Factor w/ 10 levels "G01","G02","G03",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ yield: num 6.27 5.57 8.45 7.35 6.5 6.71 5.59 8.36 7.25 8.09 ...
## $ chu : num 2.57 2.53 2.72 2.72 2.48 2.44 2.55 2.75 2.75 2.61 ...
count_na(theobald.covariate)
## year env gen yield chu
## 0 0 0 0 0
Exploratory plots:
# distributions of continuous variables
hist(theobald.covariate$yield, col = "gold")

hist(theobald.covariate$chu, col = "gray70")

# relationship between reponse variable and covariate:
with(theobald.covariate, plot(chu, yield))

length(unique(theobald.covariate$chu))
## [1] 21
# the usual boxplots:
boxplot(yield ~ env, data = theobald.covariate, col = "orangered")

boxplot(yield ~ year, data = theobald.covariate, col = "chartreuse")

boxplot(yield ~ gen, data = theobald.covariate, col = "darkcyan")

Check the extent of replication:
theobald.covariate$Year <- as.factor(theobald.covariate$year)
replications(yield ~ Year + env + gen, data = theobald.covariate)
## $Year
## Year
## 1990 1991 1992 1993 1994
## 40 63 60 45 48
##
## $env
## env
## E1 E2 E3 E4 E5 E6 E7
## 35 35 44 36 36 36 34
##
## $gen
## gen
## G01 G02 G03 G04 G05 G06 G07 G08 G09 G10
## 29 29 29 29 22 29 23 18 24 24
# with(theobald.covariate, table(gen, env, Year)) # lots of useful output
The treatments are not fully crossed, so a fully specified model of the form yield ~ Year*env*gen*chu cannot be tested. The treatments and interactions were tested in reduced models and compared (not shown). The final “best” model is shown below.
# the covariate, chu, is added in like any other effect.
theobald.lm2 <- lm(yield ~ Year + env*chu, data = theobald.covariate)
Anova(theobald.lm2, type = "III")
## Anova Table (Type III tests)
##
## Response: yield
## Sum Sq Df F value Pr(>F)
## (Intercept) 4.309 1 6.8321 0.009524 **
## Year 76.589 4 30.3607 < 2.2e-16 ***
## env 13.473 6 3.5607 0.002138 **
## chu 11.831 1 18.7596 2.187e-05 ***
## env:chu 13.376 6 3.5350 0.002268 **
## Residuals 150.096 238
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# how to extract the covariate slope(s):
emtrends(theobald.lm2, ~ env, "chu")
## env chu.trend SE df lower.CL upper.CL
## E1 7.015 1.62 238 3.82 10.21
## E2 0.979 4.44 238 -7.76 9.72
## E3 4.099 3.15 238 -2.11 10.31
## E4 -2.884 3.54 238 -9.87 4.10
## E5 8.222 2.70 238 2.90 13.54
## E6 3.425 2.72 238 -1.93 8.78
## E7 -0.359 2.55 238 -5.38 4.66
##
## Results are averaged over the levels of: Year
## Confidence level used: 0.95
# emmeans extracted as usual:
emmeans(theobald.lm2, ~ env)
## NOTE: Results may be misleading due to involvement in interactions
## env emmean SE df lower.CL upper.CL
## E1 6.67 0.175 238 6.32 7.01
## E2 5.13 0.256 238 4.63 5.64
## E3 6.66 0.482 238 5.71 7.61
## E4 7.22 0.508 238 6.22 8.22
## E5 6.61 0.138 238 6.34 6.88
## E6 6.43 0.236 238 5.97 6.90
## E7 6.32 0.397 238 5.54 7.10
##
## Results are averaged over the levels of: Year
## Confidence level used: 0.95
emmeans(theobald.lm2, ~ Year)
## Year emmean SE df lower.CL upper.CL
## 1990 6.97 0.189 238 6.60 7.34
## 1991 6.75 0.170 238 6.41 7.08
## 1992 7.07 0.187 238 6.70 7.44
## 1993 5.39 0.208 238 4.98 5.80
## 1994 6.00 0.218 238 5.57 6.43
##
## Results are averaged over the levels of: env
## Confidence level used: 0.95
Split-plot
Load “Oats” from nlme. Nitrogen level (“nitro”) is the main plot, cultivar (“Variety”) is the sub-plot and “Block” describes the blocking layout.
data(Oats)
str(Oats)
## Classes 'nfnGroupedData', 'nfGroupedData', 'groupedData' and 'data.frame': 72 obs. of 4 variables:
## $ Block : Ord.factor w/ 6 levels "VI"<"V"<"III"<..: 6 6 6 6 6 6 6 6 6 6 ...
## $ Variety: Factor w/ 3 levels "Golden Rain",..: 3 3 3 3 1 1 1 1 2 2 ...
## $ nitro : num 0 0.2 0.4 0.6 0 0.2 0.4 0.6 0 0.2 ...
## $ yield : num 111 130 157 174 117 114 161 141 105 140 ...
## - attr(*, "formula")=Class 'formula' language yield ~ nitro | Block
## .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
## - attr(*, "labels")=List of 2
## ..$ y: chr "Yield"
## ..$ x: chr "Nitrogen concentration"
## - attr(*, "units")=List of 2
## ..$ y: chr "(bushels/acre)"
## ..$ x: chr "(cwt/acre)"
## - attr(*, "inner")=Class 'formula' language ~Variety
## .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
count_na(Oats)
## Block Variety nitro yield
## 0 0 0 0
Oats$N <- as.factor(Oats$nitro)
replications(yield ~ Variety*N*Block, data = Oats)
## Variety N Block Variety:N Variety:Block
## 24 18 12 6 4
## N:Block Variety:N:Block
## 3 1
table(Oats$Variety, Oats$N)
##
## 0 0.2 0.4 0.6
## Golden Rain 6 6 6 6
## Marvellous 6 6 6 6
## Victory 6 6 6 6
hist(Oats$yield, col = "gold")

boxplot(yield ~ N, data = Oats, col = "dodgerblue1")

boxplot(yield ~ Variety, data = Oats, col = "red3")

Balanced Trial Analysis
The format for specifying split-plot error terms is Error(blocking factor/main plot).
#contrasts("contr.sum")
spl.oats <- aov(yield ~ Variety*N + Error(Block:N), data = Oats)
summary(spl.oats)
##
## Error: Block:N
## Df Sum Sq Mean Sq F value Pr(>F)
## N 3 20020 6673 7.556 0.00143 **
## Residuals 20 17663 883
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Error: Within
## Df Sum Sq Mean Sq F value Pr(>F)
## Variety 2 1786 893.2 2.930 0.0649 .
## Variety:N 6 322 53.6 0.176 0.9818
## Residuals 40 12194 304.8
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
emmeans(spl.oats, "N")
## Note: re-fitting model with sum-to-zero contrasts
## NOTE: Results may be misleading due to involvement in interactions
## N emmean SE df lower.CL upper.CL
## 0 79.4 7 20 64.8 94
## 0.2 98.9 7 20 84.3 114
## 0.4 114.2 7 20 99.6 129
## 0.6 123.4 7 20 108.8 138
##
## Results are averaged over the levels of: Variety
## Warning: EMMs are biased unless design is perfectly balanced
## Confidence level used: 0.95
emmeans(spl.oats, ~ Variety)
## Note: re-fitting model with sum-to-zero contrasts
## NOTE: Results may be misleading due to involvement in interactions
## Variety emmean SE df lower.CL upper.CL
## Golden Rain 104.5 4.55 46.1 95.3 114
## Marvellous 109.8 4.55 46.1 100.6 119
## Victory 97.6 4.55 46.1 88.5 107
##
## Results are averaged over the levels of: N
## Warning: EMMs are biased unless design is perfectly balanced
## Confidence level used: 0.95
Unbalanced Trial Analysis
spl.oats2 <- lmer(yield ~ N*Variety + (1|Block:N), data = Oats)
Anova(spl.oats2, type = "3")
## Analysis of Deviance Table (Type III Wald chisquare tests)
##
## Response: yield
## Chisq Df Pr(>Chisq)
## (Intercept) 77.1670 1 < 2.2e-16 ***
## N 13.9028 3 0.003041 **
## Variety 2.2747 2 0.320663
## N:Variety 1.0554 6 0.983423
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
emmeans(spl.oats2, "N")
## NOTE: Results may be misleading due to involvement in interactions
## N emmean SE df lower.CL upper.CL
## 0 79.4 7 20 64.8 94
## 0.2 98.9 7 20 84.3 114
## 0.4 114.2 7 20 99.6 129
## 0.6 123.4 7 20 108.8 138
##
## Results are averaged over the levels of: Variety
## Degrees-of-freedom method: kenward-roger
## Confidence level used: 0.95
emmeans(spl.oats2, ~ Variety)
## NOTE: Results may be misleading due to involvement in interactions
## Variety emmean SE df lower.CL upper.CL
## Golden Rain 104.5 4.55 46.1 95.3 114
## Marvellous 109.8 4.55 46.1 100.6 119
## Victory 97.6 4.55 46.1 88.5 107
##
## Results are averaged over the levels of: N
## Degrees-of-freedom method: kenward-roger
## Confidence level used: 0.95
Other Designs
There are many other experimental designs commonly used in agricultural trials (split-split plot, split-block, alpha lattice, etc). We have written an online resource for routine incorporation of spatial covariates into field trial analysis that includes information on how to analyze different designs. You could also consider using the agricolae package.
Extra Functions
for extracting model parameters, diagnostics and other model information
These work differently with different R object types. That is, different output will result depending on if a “lm”, “lme” or “merMod” (lmer) object is used in the function call.
# extract model summary
summary()
#extract coefficients:
coef()
#extract residuals
resid()
rstudent()
residuals()
# extract predicted values
fits()
# make diagnostic plots
plot()
# extract influence measures:
influence.measures()
#other fir diagnostics:
cooks.distance()
dffits()
dfbeta()
hat()
To see the all functions available for a particular type of linear model object, use:
methods(class = "lm") # for lm objects
## [1] add1 addterm alias
## [4] anova Anova attrassign
## [7] avPlot Boot bootCase
## [10] boxcox boxCox brief
## [13] case.names ceresPlot coerce
## [16] concordance confidenceEllipse confint
## [19] Confint cooks.distance crPlot
## [22] deltaMethod deviance dfbeta
## [25] dfbetaPlots dfbetas dfbetasPlots
## [28] drop1 dropterm dummy.coef
## [31] durbinWatsonTest effects emm_basis
## [34] extractAIC family formula
## [37] hatvalues hccm infIndexPlot
## [40] influence influencePlot initialize
## [43] inverseResponsePlot kappa labels
## [46] leveneTest leveragePlot linearHypothesis
## [49] logLik logtrans mcPlot
## [52] mmp model.frame model.matrix
## [55] ncvTest nextBoot nobs
## [58] outlierTest plot powerTransform
## [61] predict Predict print
## [64] proj qqnorm qqPlot
## [67] qr recover_data residualPlot
## [70] residualPlots residuals rstandard
## [73] rstudent S show
## [76] sigmaHat simulate slotsFromS3
## [79] spreadLevelPlot summary symbox
## [82] variable.names vcov
## see '?methods' for accessing help and source code
methods(class = "lme") # for lme4 objects
## [1] ACF anova Anova augPred
## [5] coef comparePred confint Confint
## [9] deltaMethod deviance emm_basis extractAIC
## [13] fitted fixef formula getData
## [17] getGroups getGroupsFormula getResponse getVarCov
## [21] influence intervals linearHypothesis logLik
## [25] matchCoefs nobs pairs plot
## [29] predict print qqnorm ranef
## [33] recover_data residuals S sigma
## [37] simulate summary update VarCorr
## [41] Variogram vcov
## see '?methods' for accessing help and source code
methods(class = "merMod") # for nlme objects
## [1] anova Anova as.function coef
## [5] confint cooks.distance deltaMethod deviance
## [9] df.residual drop1 emm_basis extractAIC
## [13] family fitted fixef formula
## [17] getData getL getME hatvalues
## [21] influence isGLMM isLMM isNLMM
## [25] isREML linearHypothesis logLik matchCoefs
## [29] model.frame model.matrix na.action ngrps
## [33] nobs plot predict print
## [37] profile ranef recover_data refit
## [41] refitML rePCA residuals rstudent
## [45] show sigma simulate summary
## [49] terms update VarCorr vcov
## [53] vif weights
## see '?methods' for accessing help and source code
The package emmeans also supports a large number of models.